The Einstein formula, a relation between mass and energy
Mass-energy equivalence: E=mc2
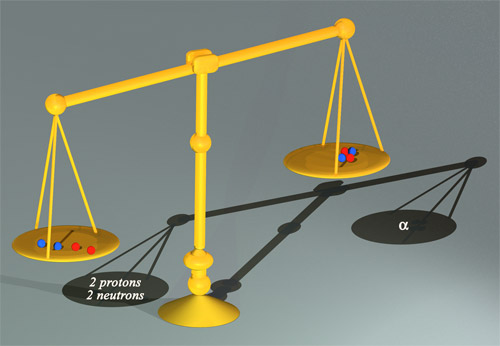
This pair of scales would show that an alpha particle is lighter than the two neutrons and two protons that make it up. This ‘mass defect’ can be translated into an energy difference by multiplying by c2. The resultant energy is known as the binding energy: in the case of two protons and two neutrons, 28 million electronvolts. This substantial value of binding energy represents less than 1% of the internal energy (or mass) of the alpha particle.
© Jean_Marc Faday (CNRS/Images-Média)
The energy released by a chemical reaction is generated by variations of ‘internal’ energies. A good example is the combustion of carbon: C + O² => CO²
The calories released by logs burning in a chimney are the result of an internal energy loss between the initial state of carbon and oxygen and the final state of carbon dioxide. Where do these ‘internal’ energies come from?
The E in Einstein’s famous equation E=MC² represents this internal energy (sometimes referred to as the mass energy) :
This energy is equivalent to the mass M of an object multiplied by the square of the speed of light c. The value of c, some 300 million meters per second, is one of the largest and most impressive natural constants. The multiplying factor of c to the square is therefore enormous. It needs only takes minuscule changes in the value of M to generate the energies we see in our chimneys, the engines of our cars, or even in our factories.
Bound nucleons in nuclei lose weight
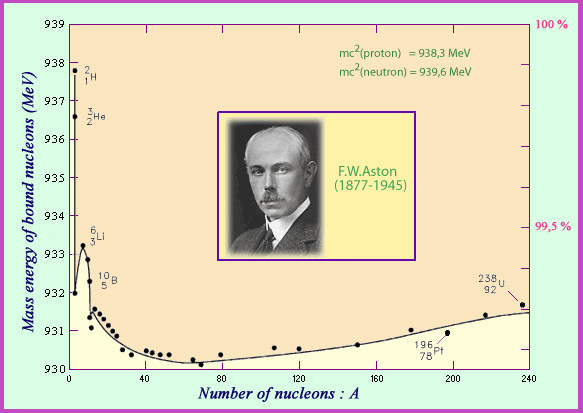
The English physicist Francis Aston was the first to measure the mass of nuclei. Dividing this mass by the number of nucleons present allows for a calculation of the average mass of a bound nucleon. Aston’s curve shows that belonging to a nucleus makes a nucleon lose just under 1% of its mass. This loss, when multiplied by the speed of light squared, comes out an energy loss which can surpass 8 million electronvolts. This is the energy that on average needs to be spent to rip a nucleon away from the nucleus: the binding energy. In the case of a nucleus, the mass lost is low but detectable, whereas in chemical phenomena involving energies of a few electronvolts the masses defects are too small to measure.
© IN2P3
In the example above, if we were to weigh the total mass of carbon and oxygen present before the reaction and compare it to the total mass of carbon dioxide produced, we would see that a tiny amount of mass is lost in the reaction. This mass difference is too small to be noticed by even the most sensitive weighing apparatus, but when multiplied by the speed of light squared it is capable of generating that friendly heat we enjoy in the fireplace.
Speed of light and relativistic particles
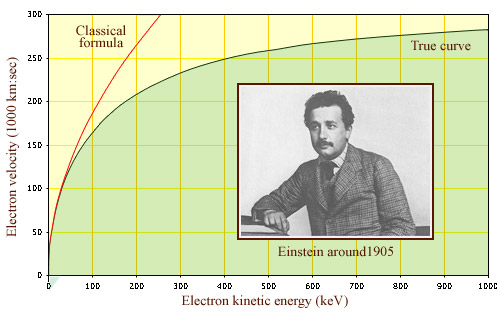
T= 1/2 mv2, the well-known formula for kinetic energy, is no longer valid for particles traveling at speeds in excess of ten thousand kilometers per second (also known as relativistic speeds). This is the case for instance of electrons produced by beta decay whose speeds approach the speed of light in vacuum (300,000 km per second). According to classical physics, no such speed limit should exist. The experimental observation that particles never travel faster than light is therefore a confirmation of the validity of the theory of relativity
© IN2P3
In the case of radioactive disintegrations and nuclear phenomena, the liberated energies are several hundreds of thousands or even millions of times larger than in chemical reactions. At these kinds of energies, the mass defects become perceptible. The mass difference between an alpha particle and the 2 protons and 2 neutrons that make it up is almost 1%. A uranium nucleus that undergoes fission therefore loses just under one thousandth of its mass.
Learn more :
Other articles on the subject « The atomic world »
The Atom
An almost empty space with mass concentrated in a tiny nucleus The atom is often viewed as a mini[...]
The electron
The best known of elementary particles The electron is an elementary particle that plays a fundam[...]
Atomic Energy Levels
A shell structure …. The conquest of space has familiarized us to the concept of a satellit[...]
Photons
The elementary components of light and electromagnetic waves Light is composed of infinitesimal i[...]
Orders of Magnitude
The very small and the very large … The atom, and the nucleus in particular, belong to the [...]
Avogadro’s Number
Trillions of billions of very small atoms …. The microscopic size of atoms comes with their[...]