The fundamental law governing radioactive decay …
The law governing the rates of radioactive decays is fundamental. When a nucleus undergoes decay through the emission of an alpha particle or a beta electron, it transforms: this allows for the conversion of radium into radon, for instance, or of tritium into helium. In such processes, however, the number of atoms in the radioactive substance inexorably dwindles. Simultaneously, however, the number of emissions per second also goes down. The decay rate is known as the activity of a particular sample, and is directly related to the number of nuclei present.
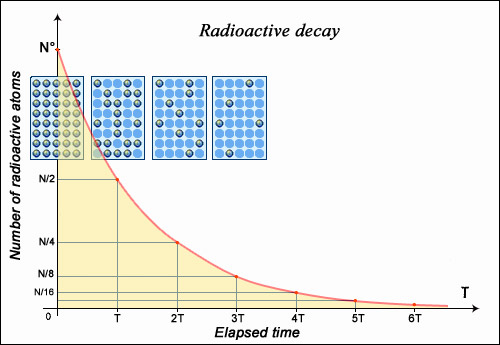
If the nucleus regains stability after having emitted a particle, the form of decay law is simple to understand: much like a currency which, every year, loses some percentage points of its ever-decreasing value. Any decay of this type is known as ‘exponential decay’, the mathematics of which are very well understood. A convenient measure of radioactive decay is a period of time known as half-life; the amount of time taken for a given sample of a substance to halve. The half-life of any substance is a characteristic property of its nucleus, and does not change.
Radioactive period or half-life:
The number of nuclei in a radioactive sample is halved after a certain characteristic period of time known as the ‘half-life’ or ‘period’. The time taken for this division does not depend on the age of the nuclei, or on the size of the sample. After two half-lives, the size of the sample is quartered (not reduced to zero), a third half-life later we are left with an eighth, and so on. This decay rate with respect to time is known as ‘exponential’, and the half-life of a nucleus is one of the most important properties of a radioactive element
© IN2P3
If the daughter nucleus (the end-result of the radiation process) is itself radioactive, then the form of decay is more complex to understand and analyse. Nevertheless, like any other such process, an eventual radioactive equilibrium is reached.
A few grams of any substance already contain millions of billions of billions of atoms; even in the smallest possible sample the number of radioactive nuclei is inconceivably great. As a result, the radioactivity is always calculated on the basis of huge numbers; even for the least radioactive of materials.

Activity of a sample of mass m and half-life T
Activities calculated in becquerels have very high values because of the value of the Avogadro number N : 6,023 followed by 23 zeros. 0,693 the neperian logarithm of 2. The half-life T expressed in seconds is obtained by multiplying T in years by 31,6 millions, the number of seconds in 1 year.
© IN2P3
All such radioactive transformations are spontaneous, random phenomena. In other words, we can never say when such disintegration is likely to occur, or which of a group of nuclei will decay first. A nucleus of Carbon-14 present in a prehistoric bone has exactly the same chance of decaying in a given time period as a nucleus from a freshly chopped tree. To put it more simply, the probability of a given nucleus undergoing radioactive decay is always constant. This probability of decaying is inseparably linked to the nucleus’s half-life, and both are among the defining properties of any radioactive material.
Articles on the subject « Radioactive decay law »
Radioactive Half-life
The half-life determines how quickly a radioisotope decays The ‘half-life’ of a radioactive nucle[...]
Radioactive Activity
The decay rate and the rate of radiation emitted The activity of a sample of radioactive matter i[...]
Radioactive Series
A long Radioactive Lineage A certain number of natural radioactive nuclei are still present on Ea[...]
Radioactive Equilibrium
An equilibrium as old as the Earth Radioactive lineage is the term given to the chain of successi[...]