A huge amount of energy at the atomic scale
The fission of a uranium or plutonium nucleus liberates a great deal of energy, energy which comes from the changes in the internal energy of the nuclei involved in the reaction. The energies involved in nuclear processes are or the order of several millions of electronvolts or MeV, to be compared to the few electronvolts released in the atomic or molecular processes of chemistry .
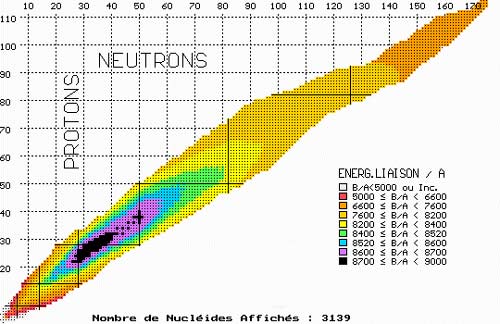
Map of nuclear binding energy
This map of nuclei is coloured accordingly to the average binding energies of its protons and neutrons – the amount of energy needed to separate its constituent nucleons divided by the number of these nucleons. The higher the binding energy, the more stable the nucleus. The most stable nucleus, iron-56, lie in the center of the black area. Uranium 235, with its 133 neutrons and 92 protons, is located in the orange zone far away from the well of stability. The two fragments formed by the fission of uranium each contain around 40 or 50 nucleons and are therefore in the more stable blue and green zones. As uranium splits, each of the 235 nucleons gains stability, each releasing 0.8 MeV of energy in the process. These 0.8 MeV combine to form the 200 MeV of kinetic energy carried away by the fission products.
© NUCLEUS
The nucleons of a uranium-235 nucleus are bound together less tightly than the smaller fission products it will split into: the binding energy of a nucleon in a uranium 235 nucleus amounting to 7.6 MeV while the binding energy of a nucleon belonging to the fission products is 8.4 MeV. This means that a nucleon of uranium-235 which ends up in a fission product releases in average 8,4 – 7,6 MeV of energy, around 800 000 electonvolts.
The energy produced by fission is obtained by multiplying this difference of 0.8 MeV by the total number of nucleons present in the fissile nucleus, 235 in the case of uranium-235. The splitting of uranium 235, for instance, releases over 200 MeV – 50 times more than the alpha decay of the same nucleus.
Over a large number of fission reactions, the liberated energy is divided in the following way:
– Kinetic energy of fission products: 165
– Kinetic energy of gamma photons 6
– Kinetic energy of neutrons 5
– Beta and gamma radiations of the fission products 11
– Energy of the invisible neutrinos: 13
Total energy released : 200 MeV
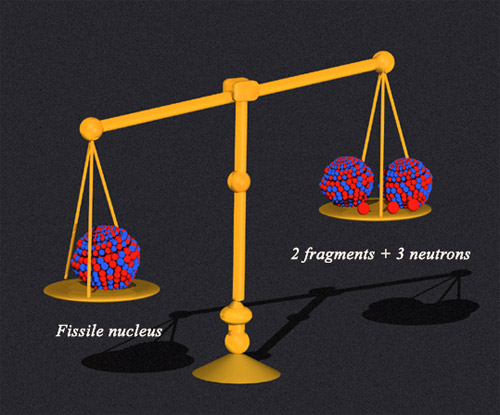
Mass-energy equivalence: E=MC2:
A nucleus of uranium 235 which splits after having absorbed a neutron is slightly heavier than the two fission products and secondary neutrons put together. This mass difference is tiny (0.2% of the total) but highly significant. When multiplied by the speed of light squared (in order to obtain its equivalent energy) the total amounts to almost 200 million electronvolts, a huge number compared to the few electronvolts of normal chemical reactions.
© Jean-Marc Faday (CNRS/Images-Média)
According to Einstein’s famous formula E=mc2, a difference in energy must result in a difference in mass. The release of 200 MeV, impressive at the atomic scale, must be accompanied by a mass diminution : the mass of the fission products is less than the mass of the fissile nucleus. The mass loss is tiny but can nevertheless be measured: if a ton of uranium 235 were to undergo fission, the total residue would weigh only 999 kilograms. This is to be compared to other other energy sources, for instance carbon combustion (coal or oil). The calculated mass defect corresponding to the combustion of 1000 tons of carbon would amount to an imperceptible quantity, 0.53 grams.
The fission of a nucleus of uranium 235 liberates the same amount of energy as the combustion of 33 million atoms of carbon, as the burning of each carbon atom releases only 6 electronvolts.
This enormous factor of 33 million is compensated by the rarity of uranium 235. Despite this rarity, nuclear energy is one of the main source of energy available to Man. The amount of nuclear energy produced could even be multiplied a hundredfold with reactors capable of burning all the uranium or thorium fuel used and not only uranium-235. The 33 million factor does help to understand why it would be difficult to obtain similar amounts of energy from other energy sources.
Other articles on the subject « Nuclear Fission »
Chain Reaction
From one single fission to fissions on a massive scale Nuclear fission emits a lot of energy on t[...]
Fissile nuclei
Uranium 235 and 233, plutonium 239 The few fissile nuclei found in nature belong to heavy atoms, [...]
Fission fragment
Chronicle of the life of a fission fragment … The fission of a nucleus into two fragments i[...]
Fission products
The ashes of nuclear fission Fission products are the remains of a heavy uranium or plutonium nuc[...]
Plutonium-239 formation
Transforming a fertile nucleus into a fissile nucleus Uranium-238 accounts for more than 95% of t[...]
Short-lived Fission Products
Most fission products vanish rather rapidly The vast majority of the radioactive fission products[...]
Long-lived Fission Products
A handful of tough but little radioactive isotopes … The more a nucleus is long-lived, the [...]
Actinides
A class of very heavy radioactive nuclei Alongside the fission products found in the core of nucl[...]
Plutonium Isotopes
Plutonium-239 but also 238, 240, 241, 242 … Plutonium isotopes are produced by neutron capt[...]
Minor Actinides
Neptunium, americium and curium Minor actinides constitute a very small minority of high activity[...]